Luis Fernando Lozano Bautista 

grupo : 303 

Obtención  cónica

La hélice cónica se define como la curva que corta a las generatrices de un cono con un ángulo constante.Las ecuaciones paramétricas de un cono son Funció a trozos: c:⎧⎩⎨⎪⎪x=s⋅costy=s⋅sentz=s⋅ctgα donde α es el ángulo que forman las generatrices con el eje del cono. Sean h:⎧⎩⎨⎪⎪x=f(t)⋅costy=f(t)⋅sentz=f(t)⋅ctgα las ecuaciones paramétricas de la hélice buscada, siendo f(t) la relación que liga los parámetros t y s de las ecuaciones del cono. Tenemos que calcular el ángulo formado por la curva y las generatrices, que viene dado en cada punto por el vector derivada de la curva y el vector director de la generatriz correspondiente. La derivada de h es: h′:⎧⎩⎨⎪⎪x′=f′(t)⋅cost−f(t)⋅senty′=f′(t)⋅sent+f(t)⋅costz′=f′(t)⋅ctgα, mientras que el vector director de cada generatriz coincide en este caso con h(t) (dada la parametrización elegida todas las generatrices pasan por el origen de coordenadas). Calculando el modulo de h y h' y el producto escalar h·h' |h|=f(t)⋅1+ctg2α−−−−−−−−√ |h′|=f′2(t)⋅(1+ctg2α)+f2(t)−−−−−−−−−−−−−−−−−−−−−√ h⋅h′=f(t)⋅f′(t)(1+ctg2α) y llamando β al ángulo formado por curva y generatrices se tiene: cosβ=h⋅h′|h|⋅|h′|=f(t)⋅f′(t)(1+ctg2α)f(t)⋅1+ctg2α−−−−−−−−√f′2(t)⋅(1+ctg2α)+f2(t)−−−−−−−−−−−−−−−−−−−−−√ Tan amenazadora expresión se queda, tras aplicar la fórmula 1+ctg2α=1sen2α y simplificar, en algo mucho más razonable: cosβ=f′(t)f′2(t)+f2(t)⋅sen2α−−−−−−−−−−−−−−−−−√ Pasando la raíz al primer miembro, elevando al cuadrado, agrupando y despejando, tenemos, aunque parezca mentira: f′(t)=f(t)⋅senα⋅ctgβ Ahora solo falta tener en cuenta que senα⋅ctgβ⋅t es constante y recordar que la función, al ser derivada, es igual a ella misma multiplicada por una constante es la exponencial para deducir que f(t)=esenα⋅ctgβ⋅t por lo que la ecuación de la hélice cónica es: h:⎧⎩⎨⎪⎪x=a⋅esenα⋅ctgβ⋅t⋅costy=a⋅esenα⋅ctgβ⋅t⋅sentz=a⋅esenα⋅ctgβ⋅t⋅ctgα donde a es un parámetro que añadimos para controlar el tamaño del cono.                     Variables y funciones. Gráficas de funciones. Ecuaciones y sistemas La calculadora Wiris incorpora las máximas facilidades (seguramente pensaréis "¡como era de esperar!") para trabajar con variables de memoria y también permite definir funciones de usuario con las mismas posibilidades que las que ya incorpora el programa. En esta actividad se comenta brevemente este hecho para pasar rápidamente a trabajar con funciones y tener el primer contacto con la Wiris como calculadora gráfica. Presentaremos el tablero grafico y veremos cuán fácil es obtener gráficas de funciones. Uso de variables y definición de funciones En un diccionario encontramos esta definición: variable. f. En programación, posición de memoria identificada con un nombre, que puede variar de contenido en la ejecución de un programa informático. En la Wiris se pueden definir variables con esta finalidad y, además, se pueden construir funciones propias que utilicen estas variables. En principio, para dar valores a las variables hay que usar el símbolo . Ahora bien, si se quieren dar a una variable valores que se actualicen cuando se modifiquen los elementos usados en la definición hay que usar el signo . Esta distinción se entenderá mejor con ejemplos y, sobre todo, cuando se hable de gràficos interactivos. Representación gráfica de funciones:   Pasamos enseguida a ver más posibilidades del comando dibujar. Modificar lo que teníamos para que diga y ya tenemos el gráfico reproducido más arriba. También es posible ordenar dos dibujos a la vez. La sintaxis es ésta:   Cuando se indica que se dibujen varios objetos con el mismo comando (en el caso anterior, dos gráficas de funciones) los atributos de dibujo seran comunes. Si queremos que sean distintos... ¡hay que distinguir!                                                           LUGARES GEOMÉTRICOS Existen dos problemas fundamentales en la Geometría Analítica: 1. Dada una ecuación hallar el lugar geométrico que representa. 2. Dado un lugar geométrico definido por determinadas condiciones, hallar su ecuación matemática. Ecuación Gráfica 1 er Problema 2° Problema CONCEPTO DE LUGAR GEOMÉTRICO Un lugar geométrico es un conjunto de puntos que satisfacen una determinada condición. La solución de un problema de lugares geométricos es una ecuación, la ecuación de todos los puntos que cumplen la dicha condición. Por ejemplo, el lugar geométrico formado por la condición 2 TABULACIÓN Es el cálculo de las coordenadas de un número suficiente de puntos (al menos diez) para obtener una  gráfica adecuada.  Por lo general, se sustituye el valor de x en la ecuación despejada para y en el paso tres. Siempre  deben darse los valores de x con base en la extensión obtenida y así obtener y , o viceversa.                                                                                       TRAZADO DE LA CURVA Una vez efectuada la tabulación, se procede a localizar los puntos encontrados en el quinto paso y  unirlos mediante una línea continua. Debe tenerse cuidado en trazar por anticipado las asíntotas (si las  hay).  Ejemplos.  Discutir las siguientes curvas, mediante el método de los seis pasos:  1) xy − 3y − 5x = 0 (1)  Solución.  • Intersecciones con los ejes  * Con respecto al eje x (y = 0) x )0( − )0(3 − 5x = 0 0 5 0 5 0 = − − x = ⇒ x = ∴ la curva corta al eje x en 0 * Con respecto al eje y (x = 0) )0( y − 3y − )0(5 = 0 0 3 0 3 0 = − − y = ⇒ y = ∴ la curva corta al eje y en 0 • Simetría  * Con respecto al eje x ( y por −y )  x(− y) − (3 −y) − 5x = 0 − xy + 3y − 5x = 0 (2) Como (1) ≠ (2), la curva no es simétrica con respecto al eje x .  * Con respecto al eje y ( x por −x )  −xy − 3y − (5 −x) = 0 − xy − 3y + 5x = 0 (3) Como (1) ≠ (3) la curva no es simétrica con respecto al eje y.  * Con respecto al origen ( x por −x ) y ( y por −y )  (−x)(−y) − (3 −y) − (5 −x) = 0 xy + 3y + 5x = 0 (4)  Como (1) ≠ (4) la curva tampoco es simétrica respecto al origen. Facultad de Contaduría y Administración. UNAM Lugares geométricos Autor: Dr. José Manuel Becerra Espinosa  5  • Extensión  * Se despeja la ecuación (1) para x :  5 3 5 3 0 5 3 ( )5 3 − − − = ⇒ − = ⇒ − = ⇒ = y y xy x y xy x y x y y x ∴ ∃ x ∀ y excepto en y = 5 * Se despeja la ecuación (1) para y :  ( ) ( ) 5 3 5 5 3 0 3 5 3 5 − − − = ⇒ − = ⇒ − = ⇒ = x x xy x y xy y x y x x y  ∴ ∃ y ∀ x excepto en x = 3 • Asíntotas  y = 5 x = 3 • Tabulación  Sustituyendo valores de x en (5) para obtener valores de y :  x -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10  y 2.5 2 1.25 0 -2.5 -10 No definido 20 12.5 10 8.75 8 7.5 7.14 PAREJAS ORDENAS  ¿Que son las parejas ordenadas ? Es una coordenada bien definida. dada por una absisa y una ordenada en el plano cartesiano por ejemplo el par ordenado ( 4, 2 ) quiere decir que la absisa es 4 y es la distancia del eje x (eje de las absisas) al eje y (eje de las ordenadas) y la ordenada es 2 e indica la distancia del eje y al eje x . Asi pues el par ordenado (4,2) es una pareja ordenada, el par ( 3, 5 ) es otra pareja ordenada, el par ( -5 , 6 ) es otra pareja ordenada. las parejas ordenadas tambien son llamadas coordenadas cartesianas en honor al matematico y padre de la geomatria analitica rene descartes, tambien son llamadas coordenadas rectangulares.ya que la ubicacion del par ordenado esta en un solo plano y a su vez el plano se divide en cuatro cuadrantes es por eso que son rectangulares un par ordenado tiene la caracteristica principal y fundamental de tener uno y solo un valor para x y un unico valor para y por tanto se dice que ( x, y ) es un par ordenado o pareja ordenada. . Ejemplo: Encuentre una pareja ordenada que es una solución de la ecuación y = x − 3, y grafique el punto en el plano coordenado. La pareja ordenada (5, 2) funciona, ya que 2 = 5 − 3. Funciones Matemáticas:  En matemática, una función (f) es una relación entre un conjunto dado X (llamado dominio) y otro conjunto de elementos Y(llamado codominio) de forma que a cada elemento x del dominio le corresponde un único elemento f(x) del codominio (los que forman el recorrido, también llamado rango o ámbito). Ver: Relaciones y funciones En lenguaje cotidiano o más simple, diremos que las funciones matemáticas equivalen al proceso lógico común que se expresa como “depende de”. Las funciones matemáticas pueden referirse a situaciones cotidianas, tales como: el costo de una llamada telefónica que depende de su duración, o el costo de enviar una encomienda que depende de su peso. A modo de ejemplo, ¿cuál sería la regla que relaciona los números de la derecha con los de la izquierda en la siguiente lista?:                           1 -------->   1                           2 -------->   4                           3 -------->   9                           4 --------> 16 Los números de la derecha son los cuadrados de los de la izquierda. La regla es entonces "elevar al cuadrado":                            1 -------->   1                           2 -------->   4                           3 -------->   9                           4 --------> 16                            x -------->   x2. Para referirse a esta regla podemos usar un nombre, que por lo general es  la letra f (de función). Entonces, f es la regla "elevar al cuadrado el número". Usualmente se emplean dos notaciones:                                            x --------> x2      o     f(x) = x2 . Así, f(3) significa aplicar la regla f a 3. Al hacerlo resulta 32 = 9. Entonces f(3) = 9. De igual modo f(2) = 4,  f(4) = 16,   f(a) = a2, etc. Veamos algunos ejemplos que constituyen funciones matemáticas. Ejemplo 1 Correspondencia entre las personas que trabajan en una oficina y su peso expresado en kilos Conjunto X Conjunto Y Ángela 55 Pedro 88 Manuel 62 Adrián 88 Roberto 90 Cada persona (perteneciente al conjunto X o dominio) constituye lo que se llama la entrada o variable independiente. Cada peso (perteneciente al conjunto Y o codominio) constituye lo que se llama la salida o variable dependiente. Notemos que una misma persona no puede tener dos pesos distintos. Notemos también que es posible que dos personas diferentes tengan el mismo peso. Ejemplo 2 Correspondencia entre el conjunto de los números reales (variable independiente) y el mismo conjunto (variable dependiente), definida por la regla "doble del número más 3".                                               x -------> 2x + 3 o bien f(x) = 2x + 3 Algunos pares de números que se corresponden por medio de esta regla son: Conjunto X Conjunto Y Desarrollo − 2 − 1 f(−2)  = 2(−2) + 3 = −4 + 3 = − 1 − 1 1 f(−1)  = 2(−1) + 3 = −2 + 3 =    1 0 3 f(0)    = 2(0)   + 3 =   0 + 3 =    3 1 5 f(1)    = 2(1)   + 3 =   2 + 3 =    5 2 7 f(2)    = 2(2)   + 3 =   4 + 3 =    7 3 9 f(3)    = 2(3)   + 3 =   6 + 3 =    9 4 11 f(4)    = 2(4)   + 3 =   8 + 3 =  11 Con estos ejemplos vamos entendiendo la noción de función: como vemos, todos y cada uno de los elementos del primer conjunto(X) están asociados a uno, y sólo a uno, del segundo conjunto (Y). Todos y cada uno significa que no puede quedar un elemento enX sin su correspondiente elemento en Y. A uno y sólo a uno significa que a un mismo elemento en X no le pueden corresponder dos elementos distintos en Y. Ahora podemos enunciar una definición más formal: Una función (f) es una regla que asigna a cada elemento x de un conjunto X (dominio) exactamente un elemento, llamado f(x), de un conjunto Y (codominio). Otra definición equivalente es: sean X e Y dos conjuntos. Una función de X en Y es una regla (o un método) que asigna un (y sólo uno) elemento en Y a cada elemento en X. Usualmente X e Y son conjuntos de números. Generalizando, si se tiene una función f, definida de un conjunto A en un conjunto B, se anota          f : A -----> B  (o, usando X por A e Y por B    f : X -----> Y) o f(x) = x Recordemos de nuevo que el primer conjunto A se conoce como dominio (Dom) de la función y B es el codominio o conjunto de llegada. f(x) denota la imagen de x bajo f, mientras que x es la preimagen de f(x). En el ejemplo 2 anterior el número 3 es la imagen del número 0 bajo f; por su parte, 1 es la preimagen del número 5. El rango (Rg) o recorrido (Rec) o ámbito (A) es el conjunto de todos los valores posibles de f(x) que se obtienen cuando x varía en todo el dominio de la función. Relaciones Entender los conceptos de Relación y de Función es de suma importancia en Matemática. Para lograr esa comprensión es necesario adentrarnos en la noción de Correspondencia, ya que esta tiene un papel fundamental en las relaciones y funciones. Lo primero es entender que Correspondencia es equivalente a Relación. En nuestra lengua, decir “en relación a”, es equivalente a decir “corresponde a”. Ejemplos: En una tienda comercial, cada artículo está relacionado con su precio; o sea, a cada artículo le corresponde un precio. En la guía telefónica, cada cliente está relacionado con un número; o sea, a cada nombre de la guía le corresponde un número.    Definición matemática de Relación y de Función En matemática, Relación es la correspondencia de un primer conjunto, llamado Dominio, con un segundo conjunto, llamadoRecorrido o Rango, de manera que a cada elemento del Dominio le corresponde uno o más elementos del Recorrido o Rango. Por su parte, una Función es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde uno y sólo un valor del Recorrido. De las definiciones anteriores podemos deducir que todas las funciones son relaciones, pero no todas las relaciones sonfunciones. También debemos agregar que toda ecuación es una Relación, pero no toda ecuación es una Función. Todas las Relaciones pueden ser graficadas en el Plano Cartesiano. Ver: Plano Cartesiano Dados dos conjuntos A y B una relación definida de A en B es un conjunto de parejas ordenadas (par ordenado) que hacen verdadera una proposición; dicho de otro modo, una relación es cualquier subconjunto del producto cartesiano A x B Ejemplo 1. Si A = {2, 3}  y B = {1, 4, 5}, encontrar tres relaciones definidas de A en B. Solución El producto cartesiano de A x B está conformado por las siguientes parejas o pares ordenados:                                         A x B = {(2, 1), (2, 4), (2, 5), (3, 1), (3, 4), (3, 5)} Y cada uno de los siguientes conjuntos corresponde a relaciones definidas de A en B:                                         R1 =  {(2, 1), (3, 1)}                                         R2 =  {(2, 4), (2, 5), (3, 4), (3, 5)}                                         R3 =  {(2, 4), (3, 5)} La relación R1 se puede definir como el conjunto de pares cuyo segundo elemento es 1, esto es, R1 =  {(x, y) / y = 1}. La relación R2 está formada por los pares cuyo primer componente es menor que el segundo componente, R2 = {(x, y) / x < y} Y la relación R3 está conformada por todos los pares que cumplen con que el segundo componente es dos unidades mayor que el primer componente, dicho de otro modo, R3 =  {(x,  y) / y = x + 2} Así, se puede continuar enumerando relaciones definidas a partir de A x B. Como se puede ver, la regla que define la relación se puede escribir mediante ecuaciones o desigualdades que relacionan los valores de x e y. Estas reglas son un medio conveniente para ordenar en pares los elementos de los dos conjuntos. Ejemplo 2. Dados los conjuntos C = {1, –3} y D = {2, 3, 6}, encontrar todos los pares ordenados (x, y) que satisfagan la relación                                      R =  {(x, y) / x + y = 3} Solución El producto cartesiano de C x D está formado por los siguientes pares ordenados                                       C x D = {(1, 2), (1, 3), (1, 6),  (–3, 2), (–3, 3),  (–3, 6)} Las parejas ordenadas que satisfacen que la suma de sus componentes sea igual a 3 son:                                      R =  {(1, 2), (–3, 6)} Toda relación queda definida si se conoce el conjunto de partida, el conjunto de llegada y la regla mediante la cual se asocian los elementos. En el ejemplo anterior, el conjunto de partida corresponde al conjunto C, el conjunto de llegada es el conjunto D y la expresión  x + y = 3  es la regla que asocia los elementos de los dos conjuntos. Dominio y rango de una relación El dominio de una relación es el conjunto de preimágenes; es decir, el conjunto formado por los elementos del conjunto de partida que están relacionados. Al conjunto de imágenes, esto es, elementos del conjunto de llegada que están relacionados, se le denomina recorrido o rango. Ejemplo 3  Sea A = {1, 2, 3, 4}  y B = {4, 5, 6, 7, 8} y R la relación definida de A en B determinada por la regla “y  es el doble de x” o  “y = 2x”, encontrar dominio y rango de la relación. Solución El total de pares ordenados que podemos formar, o producto cartesiano es: A x B =  {(1, 4), (1, 5), (1, 6), (1, 7), (1, 8), (2, 4), (2, 5), (2, 6), (2, 7), (2, 8), (3, 4), (3, 5), (3, 6), (3, 7), (3, 8), (4, 4), (4, 5), (4, 6), (4, 7), (4, 8)} Pero los pares que pertenecen a la relación R (y = 2x) son solo:                                                  R = {(2, 4), (3, 6), (4, 8)} En esta relación vemos que: “4 es el doble de 2”; esto es, “4 es la imagen de 2 bajo R”, dicho de otro modo, “2 es preimagen de 4”. Así, el dominio y rango son:                                               D = {2, 3, 4}                                               Rg = {4, 6, 8} Según lo que vemos, ¿Qué relación hay entre el Dominio y el conjunto de partida? En el Dominio falta el elemento 1 del conjunto de partida, por lo tanto el Dominio es un subconjunto de A. Otra pregunta: ¿Todo elemento del conjunto de llegada es elemento del rango? La respuesta es no, pues en el rango faltan el 5 y el 7. Representación gráfica de las relaciones Los pares ordenados se pueden representar gráficamente por medio de diagramas sagitales o por medio de puntos en el plano cartesiano. Veamos el siguiente ejemplo. Ejemplo 4 Si  A = {1, 2, 3, 4, 5} y B = {1, 3, 5, 7, 9} y  R la relación definida por la regla       R = {(x, y) / y = 2x + 1}, graficar  R. Solución Los pares ordenados que pertenecen  a la relación (que cumplen con y = 2x + 1) son:                                         R = {(1, 3), (2, 5), (3, 7), (4, 9)} Y la gráfica correspondiente es la siguiente: Ver: Funciones matemáticas Fuente Internet: http://netlizama.usach.cl/avcapituloII.pdf   Es propiedad: www.profesorenlinea.cl - Registro N° 188.540 Plano Cartesiano Dos ejes perpendiculares entre sí. El plano cartesiano está formado por dos rectas numéricas perpendiculares, una horizontal y otra vertical que se cortan en un punto. La recta horizontal es llamada eje de las abscisas o de las equis (x), y la vertical, eje de las ordenadas o de las yes, (y); el punto donde se cortan recibe el nombre de origen. El plano cartesiano tiene como finalidad describir la posición de puntos, los cuales se representan por sus coordenadas o pares ordenados. Las coordenadas se forman asociando un valor del eje de las equis a uno de las yes, respectivamente, esto indica que un punto (P) se puede ubicar en el plano cartesiano tomando como base sus coordenadas, lo cual se representa como: P (x, y) Para localizar puntos en el plano cartesiano se debe llevar a cabo el siguiente procedimiento: 1. Para localizar la abscisa o valor de x, se cuentan las unidades correspondientes hacia la derecha si son positivas o hacia la izquierda si son negativas, a partir del punto de origen, en este caso el cero. 2. Desde donde se localiza el valor de x, se cuentan las unidades correspondientes (en el eje de las ordenadas) hacia arriba si son positivas o hacia abajo, si son negativas y de esta forma se localiza cualquier punto dadas ambas coordenadas. Ver: PSU: Geometría; Pregunta 04_2005 Ejemplo: Localizar el punto A (-4, 5) en el plano cartesiano. El punto A se ubica 4 lugares hacia la izquierda en la abcisa (x) y 5 lugares hacia arriba en ordenada (y). De modo inverso, este procedimiento también se emplea cuando se requiere determinar las coordenadas de cualquier punto que esté en el plano cartesiano. Ejemplo: Determinar las coordenadas del punto M. Las coordenadas del punto M son (3,-5).                            Eje ordenadas  Unos ejes de coordenadas lo forman dos ejes perpendiculares entre sí, que se cortan en el origen. El eje horizontal se llama eje X o eje de abscisas. El eje vertical se llama eje Y o eje de ordenadas. El punto O, donde se cortan los dos ejes, es el origen de coordenadas. Las coordenadas de un punto cualquiera P se representan por (x, y). La primera coordenada se mide sobre el eje de abscisas, y se la denomina coordenada x del punto o abscisa del punto. La segunda coordenada se mide sobre el eje de ordenadas, y se le llama coordenada y del punto u ordenada del punto. Los ejes de coordenadas dividen al plano en cuatro partes iguales y a cada una de ellas se les llama cuadrante. 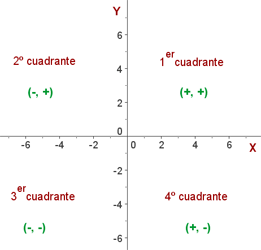Signos Abscisa Ordenada 1er cuadrante + + 2º cuadrante − + 3er cuadrante − − 4º cuadrante + − El origen de coordenadas, O, tiene de coordenadas: O(0, 0). Los puntos que están en el eje de ordenadas tienen suabscisa igual a 0. Los puntos situados en el eje de abscisas tienen su ordenada igual a 0. Los puntos situados en la misma línea horizontal (paralela al eje de abscisas) tienen la misma ordenada. Los puntos situados en una misma línea vertical (paralela al eje de ordenadas) tienen la misma abscisa. REPRESENTACIÓN GRÁFICA DE FUNCIONES Unidad 1 Representación gráfica de lugares geométricos (20 horas) Propósito de la unidad Representar gráficamente ecuaciones de las rectas y espacios geométricos poligonales, considerando principios, leyes y procedimientos de trazo, aplicables al análisis, descripción y solución de situaciones de la vida cotidiana. Resultado de aprendizaje 1.1 Representa gráficamente espacios geométricos poligonales, considera los principios, leyes y procedimientos gráficos, aplicables a la solución de situaciones de la vida cotidiana. Actividad de evaluación: Construye lugares geométricos poligonales en un sistema cartesiano, obteniendo la longitud de sus lados, medición de sus ángulos y la superficie delimitada. Evidencias a recopilar: Periódico mural, donde se expresen los conceptos básicos de la geometría analítica así como sus orígenes. Mapa o plano o croquis con polígonos ubicados, obteniendo longitudes de los lados y superficies inscritas. A.     Empleo de relaciones y funciones. ·         Variables dependientes e independientes ·         Relaciones ·         Funciones B.    Identificación de los fundamentos de la geometría analítica. ·         Segmento dirigido ·         Distancia entre dos puntos ·         Perímetro de polígonos ·         Área de polígonos ·         División de un segmento en una razón dada trazo de puntos y longitudes de sus lados  Punto medio de un segmento  Si las coordenadas de los puntos extremos, A y B, son: Las coordenadas del punto medio de un segmento coinciden con la semisuma de las coordenadas de de lospuntos extremos. Ejemplo: Hallar las coordenadas del punto medio del segmento AB.